算数ベストチェックの解説68「ひものまきつけ」

算数ベストチェックは、算数を幅広く復習するのにお勧めの教材です。

あくまで復習用なので、使い方には注意が必要です。

つまみ食いOK！未習単元に使うのはNG!算数ベストチェックの使い方

ベストチェックは良い教材なのですが、欠点は解説がほぼないことです。

ベストチェックはインプット用の教材ではないので、分からなければ他のテキストなどで学習するのが基本的な使い方です。

しかし、あれば便利でしょうから、ベストチェックの問題について解説をまとめていきます。

補助的にご利用していただければ幸いです。

68番「ひものまきつけ」(p.167・p.168)についての解説です。

ひものまきつけは、入試での出題自体はそこまで多くはありません。

出題頻度は低くても、同じパターンで解けることが多いです。

できるように取り組みましょう。

大問1　算数ベストチェックの解説68「ひものまきつけ」

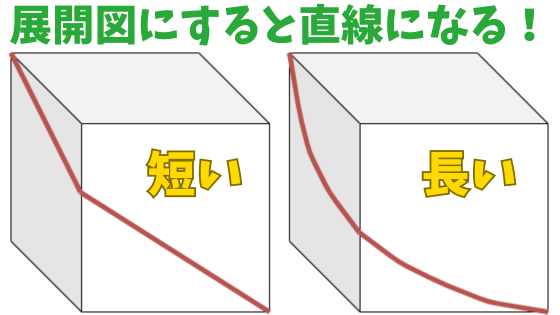
ひものまきつけの問題は、基本的に同じパターンで解くことができます。

最短となるひもは、展開図にしたときに直線になります。

たるんでいるよりも、ピンと張っている方が短くなるということです。

大問1でも、展開図を書くことが重要です。

直方体の展開図といえば、本来は6つの面があります。

しかし、ひもが通る部分以外は不要なので、ひもが通る面だけを書きます。

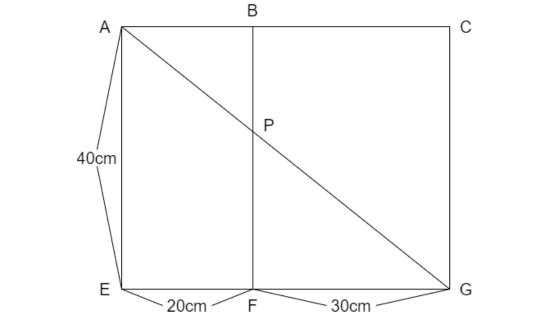
大問1では、四角形ABFEと四角形BCGFをひもが通っています。

相似の三角形が見つかります。

相似は、ベストチェックでは60番(p.152・p.153)にあります。

相似には、基本的な3つのパターンがあります。

そのうちの一つ、ピラミッド型などと呼ばれるものです。

BPとCGが平行なので、三角形ABPと、三角形ACGが相似になっています。

相似な三角形の組み合わせは、他にもあります。

三角形ABPと三角形GFPなどを利用しても構いません。

展開図を書いても相似をすぐに見つけられない場合は、相似の復習を優先しましょう。

ここでは、三角形ABPと、三角形ACGが相似を利用する場合を考えます。

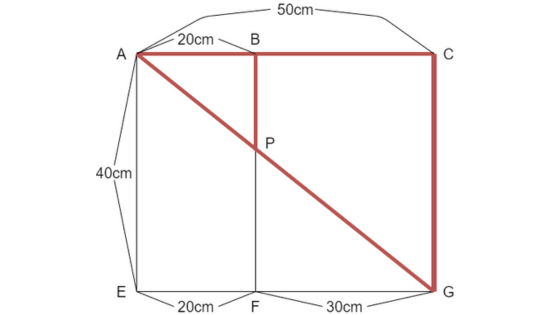
相似な三角形では、対応する辺の長さを利用して相似比を求めることが大事です。

大問1では、辺ABが20cmであり、対応する辺ACが50cmです。

相似比は20㎝:50cm=2:5となります。

相似比が分かれば、対応する辺の長さを比例式に当てはめるだけです。

BPと対応する辺はCGで、その長さは40cmです。比例式は、BP:40cm=2:5となります。

40×2÷5、または、40÷5×2で、BP=16cmと求めることができます。

なお、比例式の解き方については、ベストチェック20番(p.72・p.73)にあります。

もし比例式の解き方が分からなければ、比例式の復習を優先してください。

ポイント

• 展開図を書き、ひもを直線にする
• 相似な三角形を見つけて相似比を考える
• 比例式を使ってBPの長さを求める

大問2　算数ベストチェックの解説68「ひものまきつけ」

大問2でも、展開図を書き、ひもを直線にします。

円すいの展開図は、ベストチェック64番(p.160・p.161)にもあるように、扇形＋円になります。

底面の部分が円ですが、ひもは通らないので扇形だけを書きます。

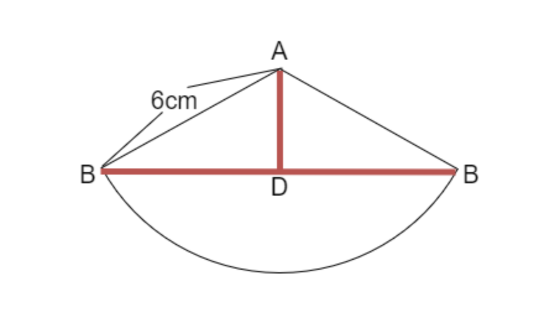
ひもは、Bから通ってBに戻るので、BとBを結ぶ直線になります。

そして、ひもの中間にDがあります。

ADの長さを求めるわけですが、分かっている長さが6cmしかありません。

長さを足したり引いたりすることでは求めることができません。

分かっている長さが少ない場合には、角度に注目することが大事です。

扇形といえば、中心角を考えることが重要です。

ベストチェック64番(p.160・p.161)にもあるように、扇形の中心角は、以下の式で求めることができます。

「半径」とは、底面の半径のことです。

母線とは、大問2のABの部分です。

ちなみに、この式に求めることができるのは、扇形の弧の長さと底面の周りの長さが一致するからです。

他の方法でも求められますが、覚えておくと便利です。

大問2では、底面の半径が2cm、母線の長さ6cmです。

中心角は以下のようになります。

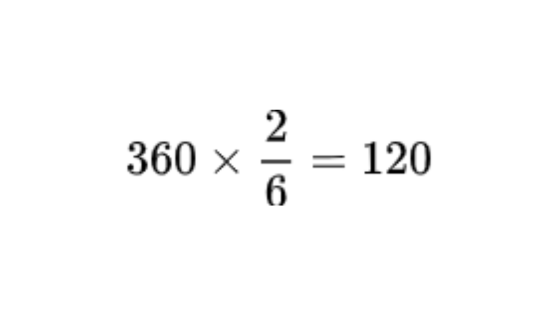
中心角が120度と分かったので、展開図に書き込みます。

120度というと、60度の2倍ですね。

直角も作れるので、60度にすることで、三角定規の形をすることができます。

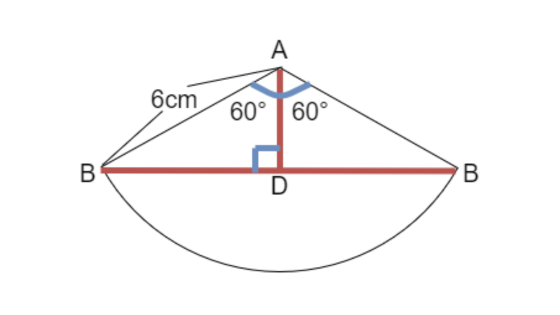
三角定規は、ベストチェック51番(p.134・135)にあるように、辺の長さに②:①の関係があります。

大問2では、6cmの部分が②、ADが①に当たります。

比例式を作ると、2:1=6:ADとなります。これを使うと、ADは3cmと求めることができます。

なお、比例式はベストチェック20番(p.72・p.73)にあります。

比例式が分からなければ、まずはそちらの復習をしてください。

ポイント

• 展開図を書き、ひもを直線にする
• 分かっている長さが少ない→角度に注目すると気付く
• 母線と底面の半径との関係を使って中心角を求める
• 三角定規の形を作って辺の長さの比を使う

大問3　算数ベストチェックの解説68「ひものまきつけ」

大問3でも、展開図を書き、ひもを直線にするのは同じです。

しかし、正四角すいの展開図は書きなれていない人が多いので、展開図を書くのが少し難しいです。

正四角すいは、底面である正方形と、4つの合同な三角形で構成されています。

底面にはひもは通らないので、4つの合同な三角形を書きます。

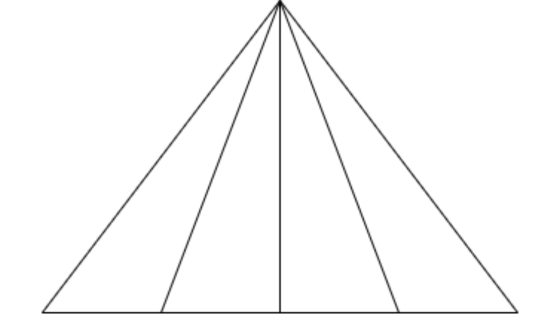
展開図を書くと、このように…なりません。

このような展開図を書く子は多いですが、典型的な誤りの例です。

正しくは、以下のような図になります。

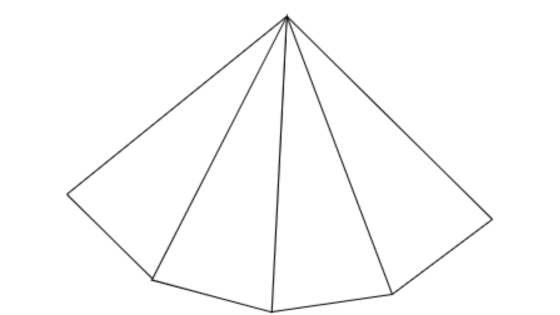
もしイメージがしにくければ、折り紙などで三角形を4つ作って並べてみてください。

展開図が完成したので、分かっている長さや角度を書き込みます。

図にはすべての数値を書き込むことが重要です。

算数・図の書き方！作図の目的は？数値をすべて書き込むのがコツ！

ひもはCから出て1周しているので、CからCを直線で結びます。

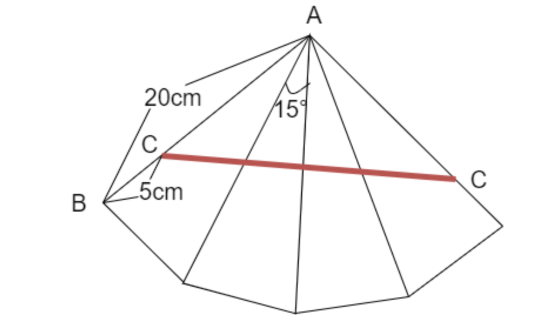
大問3でも、分かっている長さが少ないです。

角度に注目することが大事です。

三角形はすべて合同なので、15度が4つあるので、15×4で60度があることが分かります。

そして、展開図の左右にACがあるので、二等辺三角形ということが分かります。

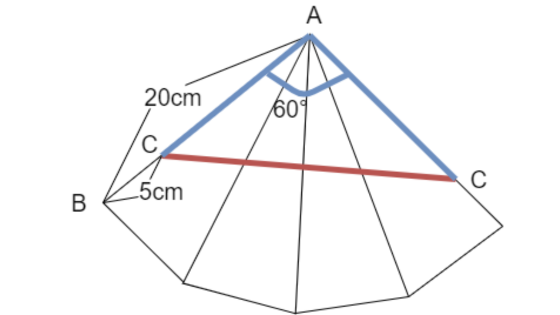
二等辺三角形であり、一つの角が60度ということは、正三角形ということです。

三角形ACCが正三角形であり、ACの長さは20-5で15cmです。

ひもの長さもACと同じということなので、15cmとなります。

ポイント

• 展開図を書き、ひもを直線にする
• 分かっている長さが少ない→角度に注目すると気付く
• 60度がある→正三角形と気付く

まとめ

「ひものまきつけ」の問題については、パターンが決まっています。

展開図を書いて、ひもを直線に書くことが重要です。

とはいえ、展開図を書いてから、実際に長さを求めるには様々な問題があります。

図を書くだけで、すぐに長さが分かることが少ないです。

長さを求めるときに、役立つ方法として相似を用いる方法があります。

相似を見つけることができれば、相似比を使って長さを求めることができます。

相似の図形は、すぐに見つけられるように練習しておきましょう。

問題で分かっている長さが少ない場合は、角度を用いる場合があります。

長さを求める問題なのに、わざわざ角度が問題に書いてあることがあります。

基本的には、答えを出すのに必要な情報しか問題にはありません。

わざわざ角度が書いてあるということは、角度を用いて長さを出す可能性が高いです。

通常は、角度だけでは長さを求めることができません。

しかし、三角定規、正三角形、または二等辺三角形などを見つければ、長さを求めることができます。

三角定規、正三角形、二等辺三角形があるのではないか、という疑いの目で問題を見ることも大事です。

算数でお困りであれば、公式LINEからお気軽にご相談ください。

また、私は家庭教師をしております。

個別指導にご興味のある方は、詳しくはこちらからご覧ください。

お読みいただき、ありがとうございます。

DMやLINE公式アカウントで個別にご相談いただけます。
Follow @twitter




「購読する」ボタンからPUSH通知を受け取ることができます。


お問い合わせは以下のフォームもご利用ください。