長方形の面積はなぜ縦×横？公式の理由・周りの長さと間違えるワケ

長方形の面積の求め方を覚えている人は多くいますよね。

しかし、「なぜ縦×横になるのか」というのを理解していないこともあります。

面積と周りの長さを間違えるということが珍しくないですが、その原因が公式の丸暗記です。

本来は、面積と周りの長さは全く異なる概念なので、間違えるはずがありません。

それでも間違えるのは、なぜ縦×横なのかを理解せず、公式を覚えているからです。

長方形に限らず、扇形などでも、面積と周りの長さを間違える人は多いです。

原因は同じです。

もっとも基本的な図形ともいえる、長方形の面積の求め方をしっかり理解することが大切です。

同じような発想で勉強すれば、扇形でも面積と周りの長さは間違えません。

長方形の面積がなぜ縦×横なのか、説明していきます。

この記事の主な対象

• 「面積と周りの長さをいつも間違えている…」という方
• 「長方形の面積が縦×横の理由を知りたい」という方

なぜ縦×横？周りの長さと間違える？長方形の面積・公式の理由は？

長方形の面積を学習するときに、

という公式を出発点として授業が展開されることがあります。

しかし、公式を出発点として勉強するのではなく、定義を出発点として勉強することが大切です。

[中学受験]算数の全分野に共通するポイント！定義が出発点！

公式を出発点とすると、「面積と周りの長さ」を間違えるというように、「すぐ忘れる」ということが起こります。

もう悩まない！算数の解き方をすぐ忘れる原因・対策

それでは、面積における定義とは何でしょうか。

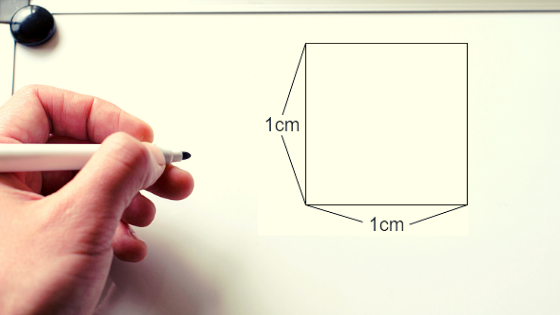
面積における定義とは、1辺が1cmの正方形の面積が1㎠ということです。

1㎠という単位は、人間が作り出したものなので、このまま覚えるしかありません。

面積は、言い換えれば「1辺が1cmの正方形が何個分か」ということになります。

例えば、「1辺が1cmの正方形が10個分」であれば、1㎠の10個分で10㎠です。

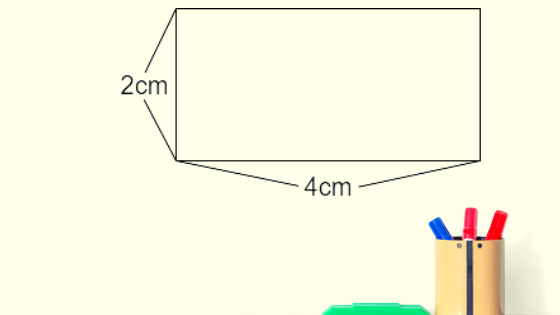
定義を確認したところで、縦が2cm、横が4cmの長方形の面積を考えます。

面積とは、「1辺が1cmの正方形が何個分か」ということなので、1辺が1cmの正方形に区切ります。

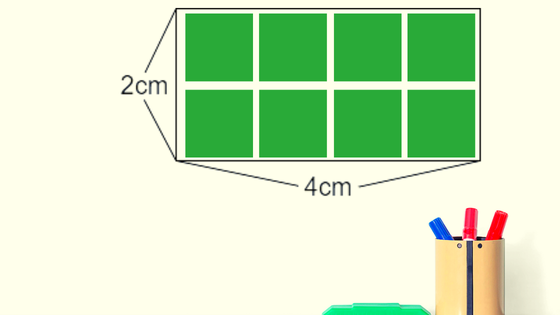
数えてみると8個分と分かるので、8㎠ということになります。

とはいえ、面積を調べるときに、毎回区切って数えていては時間がかかります。

そこで、列に分けて考えます。

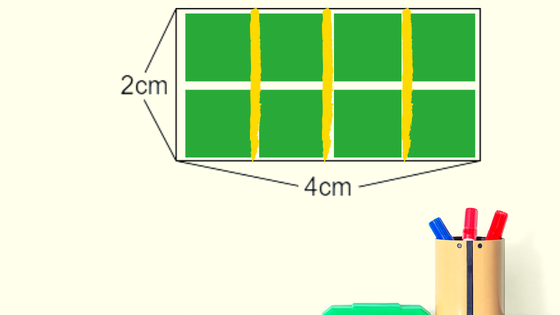
1cmずつの列に区切ると、4つの列ができます。

そして、1つの列には2個の正方形が入っています。

2個の正方形が4列あるので、2×4で8㎠ということです。

1つの列に2個あるのは、縦が2cmだからです。

また、4列あるのは、横が4cmだからです。

このような理由で、縦×横という式になります。

仕組みを理解しておけば、周りの長さと間違えることはありません。

周りの長さは求めているものが全く異なるので、列に区切るという考え方ができないからです。

まとめ

長方形の面積は、「縦×横」で求めることができます。

しかし、いきなり「縦×横」を覚えるのではなく、なぜそうなるかを理解しましょう。

算数は、公式から出発するのではなく、定義から出発することが大切です。

面積における定義とは、1辺が1cmの正方形＝1㎠です。

1辺が1cmの正方形が何個分か、というのが面積です。

長方形を列に区切って考えると、縦×横で正方形の個数を求めることができます。

このような理由で、長方形の面積は縦×横になります。

面積と周りの長さを間違える人は多いですが、原因は公式の丸暗記にあることが多いです。

扇形で間違えている場合も、原因は長方形にあることもあります。

特に面積と周りの長さを間違えたときには、なぜ縦×横になるのか、基本からきちんと確認しましょう。

算数でお困りであれば、公式LINEからお気軽にご相談ください。

また、私は家庭教師をしております。

個別指導にご興味のある方は、詳しくはこちらからご覧ください。

お読みいただき、ありがとうございます。

DMやLINE公式アカウントで個別にご相談いただけます。
Follow @twitter




「購読する」ボタンからPUSH通知を受け取ることができます。


お問い合わせは以下のフォームもご利用ください。