算数ベストチェックの解説67「特別な三角すい」

算数ベストチェックは、算数を幅広く復習するのにお勧めの教材です。

あくまで復習用なので、使い方には注意が必要です。

つまみ食いOK！未習単元に使うのはNG!算数ベストチェックの使い方

ベストチェックは良い教材なのですが、欠点は解説がほぼないことです。

インプット用の教材ではないので、分からなければ他のテキストなどで学習するのが基本的な使い方です。

しかし、あれば便利でしょうから、ベストチェックの解説をしていきます。

補助的にご利用していただければ幸いです。

67番「特別な三角すい」(p.166・p.167)についての解説です。

特別な三角すいは、ベストチェックの中では、かなり難しい部類に入ります。

実は入試での出題頻度はそこまで高くはないので、人によってはできなくても構いません。

しかし、最初から諦めるのではなく、一度は挑戦しましょう。

大問1　算数ベストチェックの解説67「特別な三角すい」

大問1は、「特別な三角すい」をそのまま出題しています。

三角すいに限らず、基本的な図形の表面積を求めるには、展開図を考えるのが定番です。

表面積とは、表面の面積＝展開図全体の面積です。

すべての面の面積を合計したものなので、展開図にすることで求めやすくなります。

例えば、円すい(ベストチェックp.160・p.161)であれば、展開図は円＋扇形になります。

つまり、円すいの表面積は、円の面積と扇形の面積を合計することで求めることができます。

[中学受験]円すいの体積は簡単なのに、なぜ表面積は難しいのか!?

表面積を求めるために、三角すいの展開図を書くことになります。

三角すいの展開図は、4つの三角形で構成されています。

4つの三角形の面積をすべて求めることができれば、表面積を求めることができます。

まず、三角形BCDは、4×4÷2=8㎠と求めることができます。

また、三角形ABD、三角形ACDは、それぞれ4×8÷2=16㎠と求めることができます。

ところが、三角形ABCは、辺の長さが一切分かっていないので面積を求めることができません。

つまり、「4つの三角形の面積を求める方法では、表面積を求めることができない」ことに気付くのがポイントです。

では、どのように求めるか、というのが「特別な三角すい」です。

特別な三角すいとは、ベストチェックp.166にあるように、展開図が正方形になる三角すいです。

大問1の三角すいも、正方形の展開図にすることができます。

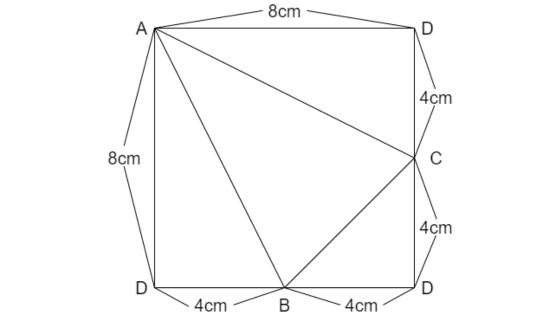
ADが8cmであり、BD＋CDも8cmです。

また、角ADC、角ADB、角BDCというDの周りの角がすべて直角になっています。

展開図にすると、正方形になります。

なぜ正方形にすることができるのかは、考えると難しいです。

特別な三角すいの問題を解けるようにするには、展開図が正方形になることを覚えるのが近道でしょう。

問題を見たときに、「特別な三角すいだ」と気付けるかがポイントです。

特別な三角すいの形を覚えることが難しければ、最終的には捨て分野にしても構いません。

展開図を書くことができれば、あとは正方形の面積を求めるだけです。

一辺が8cmなので、8×8=64㎠となります。

ポイント

• 4つの三角形の面積を求める方法では、表面積を求めることができない
• 展開図を正方形になる三角すいがある
• 正方形の展開図を書いて、その正方形の面積を求める

大問2　算数ベストチェックの解説67「特別な三角すい」

大問2では、三角すいが切り取られています。

しかし、切り取られた三角すいの形が書かれていません。

元の図形である「1辺8cmの立方体」になるように、図を補います。

すると、以下のような図になります。

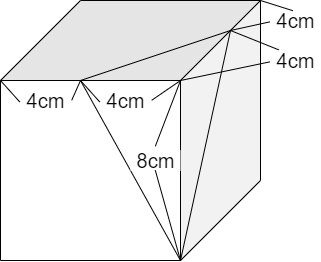
元の図形は1辺が8cmなので、切り取られた三角すいの辺の長さも分かる部分があります。

4cm、4cm、8cmという辺がありますね。

三角すいの部分だけに注目すると、以下の図になります。

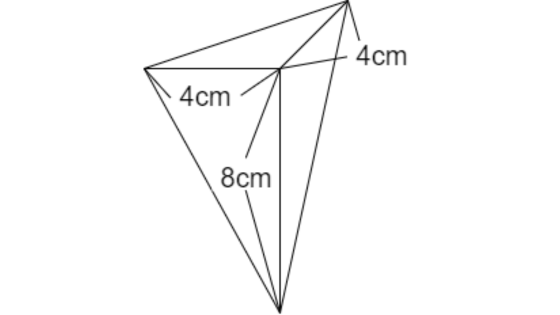
大問1の三角すいを逆さにした形ですね。

辺の長さも同じなので、切り取られた三角すいは、大問1の三角すいと同じということです。

表面の面積を考えるためには、元の図形からの変化を考えることがポイントです。

立方体から三角すいを切り取ることによって、どのように表面積が変化するか、ということです。

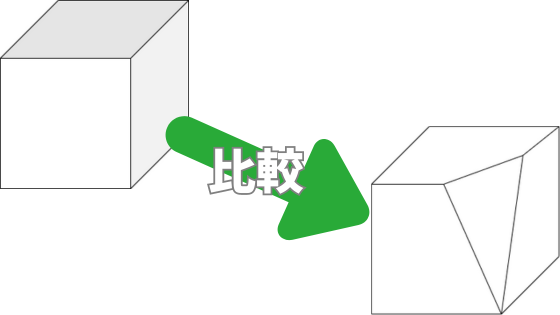
比較してみると、切り取ったことによってなくなった面があります。

また、切り取ったことによって新たに誕生した面もあります。

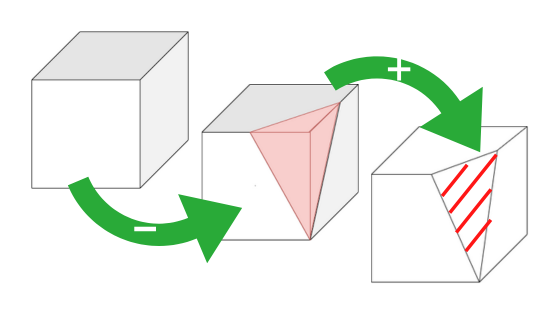
立方体から、赤い部分である3つの面がなくなり、赤い斜線の面が新たに誕生しています。

まずは、立方体の表面積から、なくなった3つの面の面積を引きます。

そのうえで、新たに誕生した面の面積を加えることで、大問2の立体の表面積を求めることができます。

立方体の表面積は、8×8×6=384㎠です。

なくなった3つの面は、直角三角形なので面積を求めることができます。

しかし、新たに誕生した面の面積をどのように求めるかが問題になります。

大問1と同様に、展開図を作って考えます。

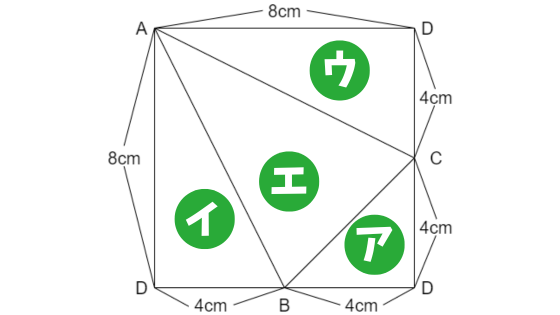
大問1と同じ三角すいなので、展開図も同じものです。

ア・イ・ウの部分がなくなった面積で、エの部分が新たに誕生した部分です。

アの面積は、4×4÷2=8㎠、イ・ウの面積は、4×8÷2＝16㎠です。

エの部分は、正方形からア・イ・ウを引くことで求めることができます。

エの面積は、8×8-(8+16×2)=24㎠です。

そして、立方体-(ア＋イ＋ウ)＋エで求めることができます。

答えは、384-(8＋16＋16)＋24=368㎠です。

ポイント

• 切り取られた三角すいの形を考える
• 切り取ることによる表面積の変化を考える
• 三角すいの展開図を使って変化した部分の面積を求める

大問3　算数ベストチェックの解説67「特別な三角すい」

 四角すいの体積は、底面積×高さ×3分の1で求めるのが基本的な方法です。

ところが、大問2の四角すいは高さが分かりません。

「底面積×高さ×3分の1」という公式では求めることができません。

四角すいの展開図を4つの正方形に区切ります。

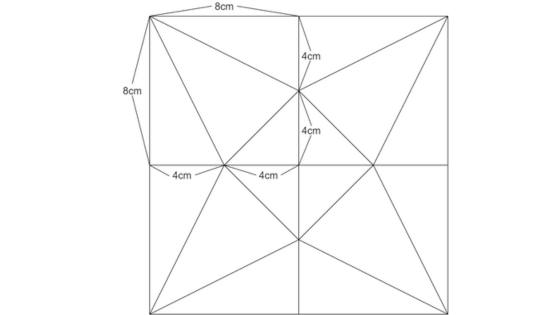
左上の正方形に注目すると、大問1や大問2の展開図と全く同じになっています。

つまり、大問3の四角すいは、三角すいを4つ集めた図形ということです。

三角すいの体積を4倍すれば、求めることができます。

1つの三角すいは、以下のような図になります。

三角すいの体積は、底面積×高さ×3分の1で求めることができます。

「4×4÷2×8×1/3=21と1/3」となります。

この3角すいの4倍なので、21と1/3×4=85と1/3㎠が答えです。

ポイント

• 公式「底面積×高さ×3分の1」だけでは求めることができない
• 展開図を4つに区切り、3角すいの4倍と気付く

まとめ

特別な三角すいは、言葉の通りに「特別な」三角すいです。

特別なので、「特別な三角すいを使う」と気付けない限り、解くことが難しいです。

また、特別なので入試での出題も限られます。

できなくても大きな痛手にはなりません。

もちろん、できることが望ましいのです。

しかし、特別な三角すいは難しいので、最終的にはできなくても構いません。

何回か挑戦して、難しければ他に時間を使う方が効率的でしょう。

とはいえ、せっかくなので、ポイントをまとめておきます。

特別な三角すいは、展開図が正方形になる三角すいです。

正方形の展開図を書くことで、すべての面の面積を求めることができます。

また、特別な三角すいを組み合わせた四角すいの体積も求めることができます。

ベストチェックはあくまで復習用の教材なので、分からなければ他のテキストなどで学習しましょう。

しかし、特別な三角すいについては、優先度が下がるので、後回しでも構いません。

算数でお困りであれば、公式LINEからお気軽にご相談ください。

また、私は家庭教師をしております。

個別指導にご興味のある方は、詳しくはこちらからご覧ください。

お読みいただき、ありがとうございます。

DMやLINE公式アカウントで個別にご相談いただけます。
Follow @twitter




「購読する」ボタンからPUSH通知を受け取ることができます。


お問い合わせは以下のフォームもご利用ください。