[中学受験]円すいの体積は簡単なのに、なぜ表面積は難しいのか!?

中学受験の算数では、円すいの体積は定番の問題です。

体積を求めるだけの問題であれば、模試でも正解率が高くなります。

円すいの体積を学習するのとほぼ同じ時期に、表面積も学習します。

ところが、表面積については正解率が低くなります。

円すいの体積を求める問題は簡単なのに、表面積は難しいと感じる子が多いです。

表面積を学習する際は、間違えやすいポイントがあると意識しながら学習することが望ましいです。

この記事の主な対象

• 「円すいの体積はできるのに、表面積は間違えてばかり…」という方
• 「円すいの体積も表面積も同じように勉強すればいいんじゃないの？」という方

円すいの体積は簡単なのに、なぜ表面積は難しいのか!?

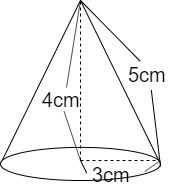
母線の長さが5cm、高さが4cm、底面の半径が3cmの円すいを用います。

体積の求め方と、表面積の求め方を比較していきます。

なお、円周率は3.14とします。

体積

体積は、以下の式で求めることができます。

つまり、

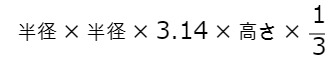
です。

問題の数値を当てはめると、

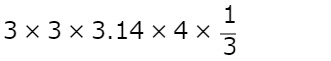
となり、37.68と求めることができます。

円すいの体積は、問題の図にある数値をそのまま公式に当てはめるだけで求めることができます。

表面積

では、表面積の場合はどうでしょうか。

表面積とは立体の表面の面積ですから、展開図にしないと分かりにくいです。

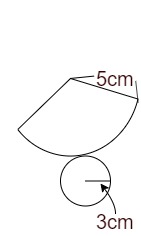
展開図にすると、おうぎ形の面積と円の面積を加えればよいと分かります。

少なくとも慣れるまでは、自分で展開図に書き換える必要があるというのが、表面積が難しい理由の一つです。

おうぎ形の面積と円の面積を求めることになりますが、おうぎ形の面積は以下の式で求められます。

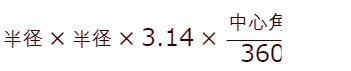
ところが、中心角は問題の図には書いてありません。

中心角を自分で求める必要があるというのが、もう一つの難しい理由です。

ちなみに、「中心角/360」と「底面の半径/母線の長さ」は同じです。

おうぎ形の面積は、5×5×3.14×3/5となります。

これに円の面積である3×3×3.14を加えると、24×3.14=75.36となります。

このように、3.14が複数回登場して、計算がややこしいというのも難しい理由です。

計算を楽にして間違えにくくするためにも、できるだけ早い段階で分配法則を身に付けておくことも重要です。

中学受験専門家庭教師が教える！分配法則が重要な理由

まとめ

中学受験の算数において、円すいの体積や表面積は、基本事項です。

体積は簡単に求めることができても、表面積は難しいと感じる子が多いです。

体積は、問題にある数値を公式に当てはめる事で計算ができるので、難しくありません。

しかし、表面積の場合は、以下の3つの理由により、難しくなります。

1. 展開図に書き換えないと分かりにくい
2. おうぎ形の中心角が問題の図には書かれてない
3. 計算が複雑

難しいポイントがあるからこそ、しっかり練習していきましょう。

「体積はできるのに、表面積ができないのはおかしい」と、お子さんを怒らないでくださいね。

お子さんにとっては、表面積はとても難しく感じているはずです。

円すいを含めて算数でお困りであれば、公式LINEからお気軽にご相談ください。

また、私は家庭教師をしております。

個別指導にご興味のある方は、詳しくはこちらからご覧ください。

お読みいただき、ありがとうございます。

DMやLINE公式アカウントで個別にご相談いただけます。
Follow @twitter




「購読する」ボタンからPUSH通知を受け取ることができます。


お問い合わせは以下のフォームもご利用ください。