算数ベストチェックの解説69「水位と比」

算数ベストチェックは、算数を幅広く復習するのにお勧めの教材です。

あくまで復習用なので、使い方には注意が必要です。

つまみ食いOK！未習単元に使うのはNG!算数ベストチェックの使い方

ベストチェックは良い教材なのですが、欠点は解説がほぼないことです。

ベストチェックはインプット用の教材ではないので、分からなければ他のテキストなどで学習するのが基本的な使い方です。

しかし、あれば便利でしょうから、ベストチェックの問題について解説していきます。

補助的にご利用していただければ幸いです。

69番「水位と比」(p.170・171)についての解説です。

入試問題では、「水位と比」単体での出題は少ないです。

比を使わなければ解けない問題は多くありません。

しかし、比を使うと便利な問題は多いので、できることが理想的ではあります。

もちろん、明確に比を使うことを求められていない場合は、比を使う必要はありません。

難しければ、比を使わなくても構いませんが、まずは挑戦してみましょう。

大問１　算数ベストチェックの解説69「水位と比」

逆比・反比例を使う方法と、逆比・反比例を使わない方法があります。

逆比・反比例を使うと計算は楽になりますが、分かりにくいと感じる子も多いはずです。

まずは、逆比・反比例を使わない方法から説明します。

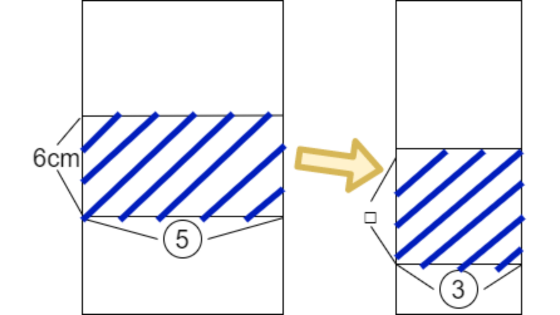
直方体の容器は、断面図を書くと長方形になります。

水の形も長方形になるので、水の体積を面積のように計算することができます。

Aの容器から移される水は半分なので、12÷2で深さ6cmの部分です。

体積は、底面積×高さで求めることができます。

底面積が何㎠かは分かっていません。

丸の5をそのまま使い、5×6をします。

すると、Aの容器から移される水の体積は30となります。

30の水がBに移ると、底面積が丸の3になります。

30という体積は変わらないので、底面積×高さ=体積という式を再び使います。

高さは分からないので、増える部分の高さを□とします。

3×□=30となり、30÷3で□は10cmです。

最後に元々の3cmを加えると、3＋10で答えは13cmになります。

水の体積を面積のように考えることは、逆比・反比例を使う方法でも同じです。

長方形の面積は、縦×横という積の形です。

そして、水をAからBに移しても、体積は変わりません。

断面図においては、面積が同じになるということです。

面積は積の形なので、積が等しいということです。

このように、積が等しい場合には、逆比・反比例を使うことができます。

大問1で等しい積は、「底面積」×「高さ」です。

「底面積の比」と「高さの比」が逆比になります。

ちなみに、ベストチェックでは、22番(p.76・77)で逆比について扱われています。

逆比と反比例というのは実質的に同じことです。

底面積の比は5:3です。

高さの比は6:□です。

逆比になるので、5:3=□：6という比例式(ベストチェック20番(p.72・73))になります。

比例式を使って計算すると、□は10となります。

または、6×5/3で10と求めることができます。

最後は、3＋10で答えは13cmになります。

ポイント

• 面積のように考える
• 底面積の比を使って底面積×高さを計算する、または底面積と高さの逆比・反比例を使う

大問２　算数ベストチェックの解説69「水位と比」

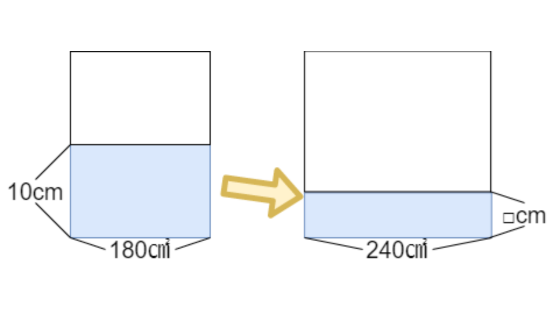
まずは、比を使わない方法から説明します。

大問１と同じように、断面図を書いて面積のように考えます。

ただし、断面図を書かなくても体積を求められる人は、断面図を書く必要はありません。

倒す前の底面積は、12×15で180㎠です。

水の深さが10cmなので、180×10で水の体積は1800㎤です。

倒されても水の体積は変わりません。

倒されると、底面積が20×12で240㎠になります。

体積は1800㎤なので、1800÷240で深さは7.5cmになります。

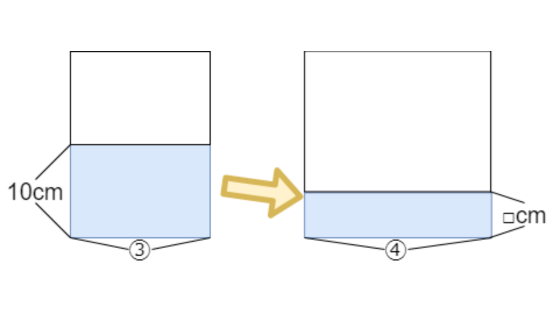
比を使う場合は、まずは底面積の比を求めます。

倒す前の底面積は180㎠で、倒した後の底面積は240㎠です。

底面積の比は、180:240=3:4になっています。

そして、倒しても水の体積は変わらないので、積が一定ということです。

積が一定であれば、逆比を使うことができます。

水の体積は、底面積×高さなので、「底面積の比」と「高さの比」が逆比になります。

高さは倒す前が10cmで、倒した後を□とします。

3:4=□:10で□は7.5cmになります。

ポイント

• 面積のように考える
• 底面積×高さを計算する、または底面積と高さの逆比・反比例を使う

大問３　算数ベストチェックの解説69「水位と比」

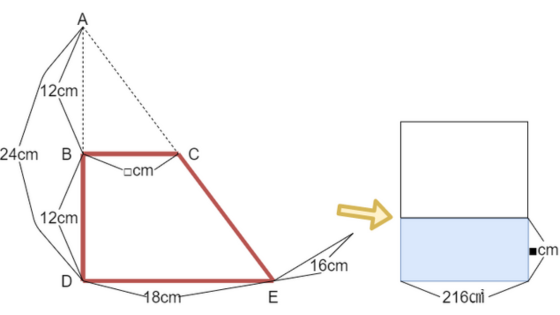
まずは、比を使わない場合について述べていきます。

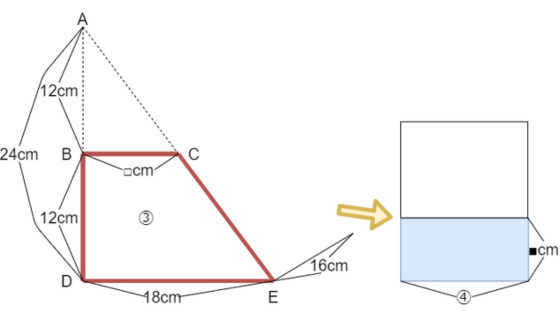
台形の部分を底面積、16cmを高さと考えることで、水の体積を求めることができます。

台形の面積を求める必要があるので、説明のために図のようにABCDEを定めます。

三角形ABCと三角形ADEが相似(ベストチェック60番(p.152・153))になっています。

ABは24-12で12cmなので、相似比は12:24=1:2です。

□:18=1:2より、BCは9cmです。

台形の面積は、(9＋18)×12÷2で162㎠です。

水の高さは16cmなので、水の体積は162×16で2592㎤です。

容器を倒すと、底面積が三角形の部分になります。

18×24÷2で底面積は216㎠です。

倒しても水の体積は変わらないので、2592÷216で深さは12cmになります。

次に、比を使う方法を述べますが、比を使う方法も複数あります。

先ほどと同様に、162㎠と216㎠を求めてから、162:216=3:4と底面積の比を求めるのが一つの方法です。

もう一つは、ベストチェックp.170のように、相似比から面積比を求める方法です。

三角形ABCと三角形ADEの相似比は1:2なので、面積比は1×1:2×2で1:4になります。

台形は、三角形ADEから三角形ABCを除いた部分なので、4-1の3に相当します。

台形と三角形ABCの面積比は3:4というのは同じです。

そして、倒しても水の体積は変わらないので、積が一定、つまり逆比を使うことができます。

これまでと同様に、「底面積の比」と「高さの比」が逆比になります。

底面積の比は3:4なので、3:4=■:16で12cmと求めることができます。

ポイント

• 台形の部分を底面積と考える
• 台形の部分は相似を利用して面積を求める、または面積比を求める
• 底面積×高さを計算する、または底面積と高さの逆比・反比例を使う

大問４　算数ベストチェックの解説69「水位と比」

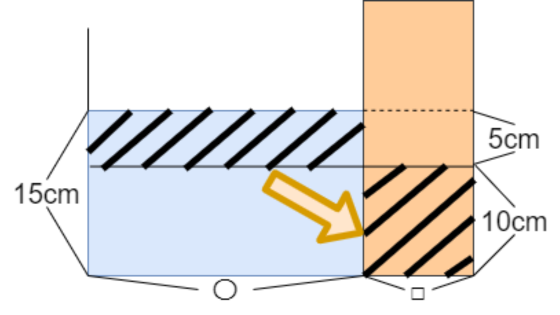
水の中に棒などを入れる問題の場合は、棒が端にある図の方が見やすくなります。

棒を右端に動かして図を変えました。

書き直さなくても解ける人は、書き直す必要はありません。

大問４は、比を求める問題なので、比を使わない方法では解けません。

容器から棒を除いた部分の底面積を○、棒の底面積を□とします。

棒を抜いたことによって、左上にあった水が右下に移動しました。

つまり、左上の斜線部と右下の斜線部は体積が同じです。

体積が同じということは、「底面積の比」と「高さの比」が逆比になります。

高さは5cmと10cmなので、5:10=1:2です。

2:1＝○:□となります。

容器の底面積は、○＋□なので、答えは、2＋1:1で3:1となります。

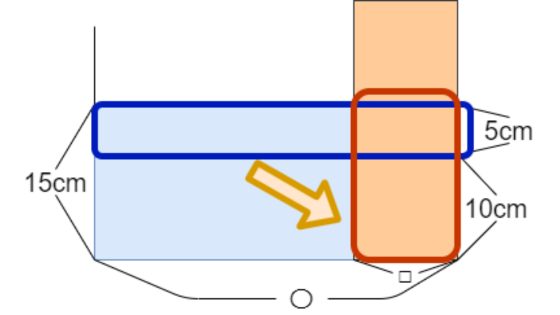
先ほどの斜線部両方に右上の部分を加えて、大きい長方形にする方法もあります。

こうすると、容器の底面積をそのまま○にすることができます。

濃い青の部分と濃い赤の部分が等しくなるので、「底面積の比」と「高さの比」が逆比になります。

高さは5cmと15cmなので、高さの比は5:15=1:3です。

逆比で、3:1が答えになります。

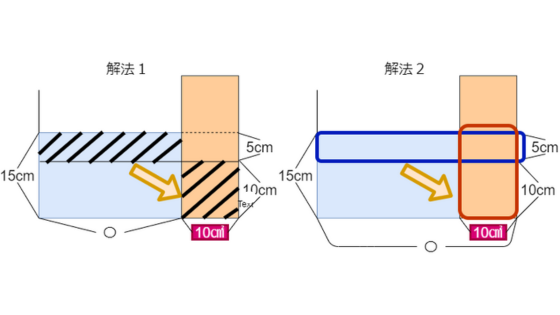
比を使うのが複雑だと感じることも多いでしょう。

大問４では、一切面積が登場しません。

これを逆手に取って、自分で勝手に面積を決めてしまう方法もあります。

面積に関する情報がないということは、面積がいくつでも答えが同じになるということです。

棒の底面積を10㎠としてみます。

最初の解法１では、右下の体積が10×10で100㎤になります。

体積が同じなので、100÷5で○は20㎠になります。

容器の底面積は20＋10で30㎠です。30㎠と10㎠なので、30:10=3:1と同じ答えになります。

次に、解法２では、赤い部分の体積が10×15で150㎤になります。

青い部分も同じ体積なので、150÷5で○は30㎠になります。

30:10=3:1で、こちらも同じ答えになります。

棒の底面積を10㎠にしましたが、数字を変えても答えは同じになります。

数字を変えて何回か計算してみると、納得できるでしょう。

数字は何でも構いません。

勝手に底面積を決めることで、逆比を避けることができます。

ポイント

• 同じ体積の場所を見つけて逆比・反比例を使う、または勝手に底面積を決めることで逆比を回避する

まとめ

大問４以外は、比を使う方法と比を使わない方法があります。

比を使うと、式の数は減りますし、数字も小さくなって計算が楽になります。

ミスもしにくくなるし、早くできるというメリットがあります。

しかし、比の使い方を理解できているのが前提になります。

比は抽象的ですから、理解するのが難しいです。

比を使うことが明示的に求められている問題以外は、無理に比を使う必要はありません。

比を使おうとしても間違えるぐらいなら、使わない方が良いです。

大問４に関しては、比を使う以外に方法がありません。

しかし、勝手に具体的な数字を決めることで考えやすくなります。

比は抽象的な数字なので、できるだけ具体的な数字を使うと解きやすくなります。

特に、逆比は抽象的ですから、小学生に理解を要求するのはややレベルが高いです。

具体的な数字を使うことで、逆比を避けられるというメリットは大きいです。

いずれにしても、複数の解き方があり、どれか一つが正解というものではありません。

試行錯誤しながら、最適な方法を身に付けていきましょう。

算数でお困りであれば、公式LINEからお気軽にご相談ください。

また、私は家庭教師をしております。

個別指導にご興味のある方は、詳しくはこちらからご覧ください。

お読みいただき、ありがとうございます。

DMやLINE公式アカウントで個別にご相談いただけます。
Follow @twitter




「購読する」ボタンからPUSH通知を受け取ることができます。


お問い合わせは以下のフォームもご利用ください。