算数ベストチェックは、算数を幅広く復習するのにお勧めの教材です。
あくまで復習用なので、使い方には注意が必要です。
つまみ食いOK！未習単元に使うのはNG!算数ベストチェックの使い方
ベストチェックは良い教材なのですが、欠点は解説がほぼないことです。
ベストチェックはインプット用の教材ではないので、分からなければ他のテキストなどで学習するのが基本的な使い方です。
しかし、あれば便利でしょうから、ベストチェックの問題について解説していきます。
補助的にご利用していただければ幸いです。
70番「水そうグラフ」(p.172・173)についての解説です。
水そうグラフは、やや応用的な問題ではありますが、入試ではよく出題されます。
入試での出題は、難易度も様々ですが、ベストチェックのような問題はできることを目指したいですね。
大問１ 算数ベストチェックの解説70「水そうグラフ」
大問１（１）
水そうの問題は、断面図(正面から見た図)を書くと分かりやすくなります。
グラフを見ると、アの部分の水位が最初から上がっています。
つまり、アの部分に水を入れていることが分かります。
そして、アの部分に水が貯まると、水があふれてイの部分に流れていきます。
イの部分に水が貯まっている時間は、アの水位は変化しません。
このように考えると、アの部分に水が入るのにかかった時間が8分、イの部分が20-8で12分と分かります。
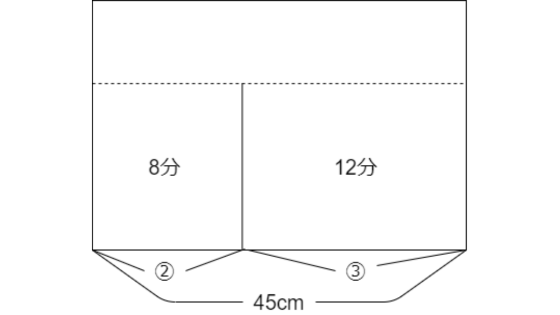
比を使うと楽な計算で答えにたどり着くことができます。
アの部分とイの部分に水が入る時間が8:12=2:3です。
水が入る時間と、水が入る量は比例します。
また、高さと縦が同じ場合、横の長さと体積が比例します。
アの部分とイの部分の横の長さも、2:3になっているということです。
比が分かれば、比例配分(ベストチェック21番(p.74・75))することができます。
45×3/(2＋3)で答えは27cmです。
比を使うのが難しければ、体積を使って解くこともできます。
アとイの部分を合わせた体積は、29×45×22で28710㎤です。
20分で水が入っているので、28710÷20で、1分あたり1435.5㎤の水が入っています。
イの部分は12分で水が貯まっているので、1435.5×12の17226㎤と分かります。
直方体の体積は、縦×横×高さなので、29×AB×22が17226ということです。
17226÷29÷22で、答えは同じく27cmになります。
比を使うよりも計算の手間は増えますが、人によっては考えやすくなるでしょう。
大問１（２）
「うちのり」という言葉に馴染みがないお子さんは多いでしょう。
「うちのり」というのは、内側の高さということです。
実際の水そうには厚みがあるので、内側の高さと外側の高さは異なります。
しかし、算数の水そうでは、厚みを考えない問題が多いので、「うちのり」という言葉はあまり気にする必要はありません。
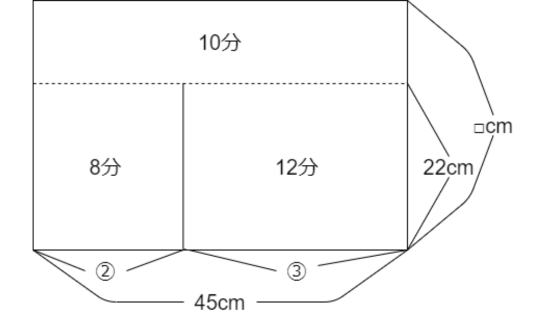
20分で22cmの高さまで水が入ってからは、上の部分に水が入っていきます。
そして、30分後に満水になるので、上の部分は30-20で10cmです。
アとイの部分を合わせた部分と、上の部分は、底面積が同じです。
水の体積・水を入れる時間と、高さが比例します。
水を入れる時間は、20分:30分=2:3です。
2:3=22cm:□cmという比例式(ベストチェック20番(p.72・73))になり、答えは33cmです。
比を使わない場合は、先ほどと同じように、「1分あたり1435.5㎤」というのを使います。
全体が30分で満水なので、1435.5×30で水そうの体積は43065㎤です。
縦が29cm、横が45cmなので、43065÷29÷45で答えは同じく33cmと求めることができます。
ポイント
- 断面図を書く
- どの部分に何分で水が入るかを考える
- 比例配分、または1分あたりに入る水の量を計算する
大問２ 算数ベストチェックの解説70「水そうグラフ」
大問２（１）
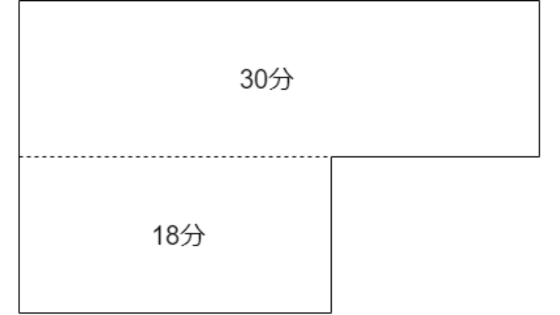
グラフを見ると、18分から上がり方が緩やかになっています。
緩やかになったのは、広い部分に水が入るようになったからです。
18分で下の部分が満たされて、そこから先は上の部分に水が増えていくということです。
下の部分は18分、上の部分は48-18の30分で満たされています。
そして、水を入れる時間と、水が入る量は比例します。
時間が18:30なので、水の量も18:30=2:5ということです。
大問２（２）
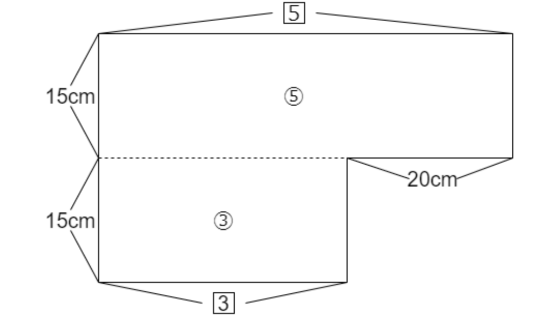
グラフから、下の部分の高さが 15cm、上の部分の高さが30-15で15cmと分かります。
上の部分と下の部分の高さが同じということです。
高さが同じで、縦の長さも同じなので、体積と横の長さが比例します。
なぜ比例するのか分からない場合は、速さと比(ベストチェック27番(p.86・87))などをよく復習しましょう。
体積の比が2:5なので、横の長さも2:5になります。
5-3で2の部分が20cmですから、20×5/2で50cmになります。
ポイント
- 断面図を書く
- どの部分に何分で水が入るかを考える
- 体積の比と横の長さの比が等しくなることを使う
まとめ
大問１は比を使う方法もあれば、比を使わない方法もあります。
一方、大問２は基本的には比を使う以外に方法がありません。
大問２では、横の長さが分からず、体積を求めることができないからです。
複数の場所の長さが関係してくるので、長さを勝手に自分で決めるということもできません。
大問１と大問２に違いはありますが、いずれにしても、水そうの問題は、断面図を書くことで考えやすくなります。
大問１についても、比を使えると計算が楽になるので理想的ではあります。
しかし、無理に比を使おうとして間違えたら意味がありません。
分かりにくいのであれば、比を使わない方法でも構いません。
比を使わなくても解けることがあるのは、ベストチェック69番と同様です。
水そうグラフの問題は、入試でもよく出題されます。
ベストチェックの問題が解ければ、銀本などを使って練習しましょう。
水そうグラフについて出題された入試問題についても解説しています。
実際に解いた際に、是非ご利用ください。
算数でお困りであれば、公式LINEからお気軽にご相談ください。
また、私は家庭教師をしております。
個別指導にご興味のある方は、詳しくはこちらからご覧ください。
DMやLINE公式アカウントで個別にご相談いただけます。
Follow @twitter
「購読する」ボタンからPUSH通知を受け取ることができます。
お問い合わせは以下のフォームもご利用ください。
