算数では、様々なグラフが登場します。
棒グラフ、折れ線グラフ、円グラフや帯グラフが登場します。
棒グラフや折れ線グラフの問題ができるのに、円グラフはできないという子は珍しくありません。
小学生にとって、円グラフは難しいんです。
円グラフが難しいのは、数量がそのまま表示されないことに理由があります。
棒グラフであれば、例えば目盛りを5つ数えれば「5人」を表すことができます。
折れ線グラフであっても、目盛りを5つ数えて他の点と結べばグラフができます。
一方、円グラフでは「5人」を表示するために、目盛りを5つ取ることはできません。
円を区切って表示するので、「5人」をそのままの数字ではなく、角度に変換する必要があります。
どのように角度に変換していくのか、述べていきます。
算数で円グラフが難しい理由
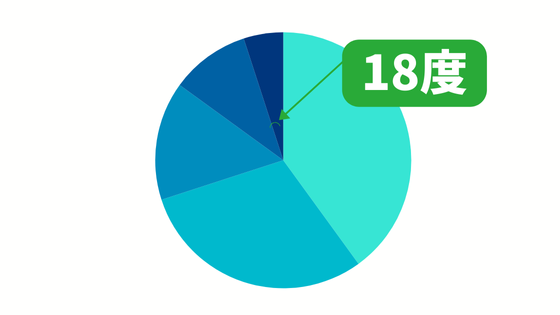
円グラフとは、円を扇形に分割するグラフです。
棒グラフであれば、棒が長ければ量が多いと分かります。
また、折れ線グラフであれば、線が上がっていれば量が増えていると分かります。
一方、円グラフは、扇形が大きければ量が多いと分かります。
つまり、円グラフを作る際には、どの程度の大きさの扇形にするかを考える必要があります。
扇形の大きさは、弧の長さや、中心角に比例します。
面積を求めるときにも、弧の長さを求めるときも、中心角を用いますね。
扇形が大きければ、弧の長さも長いですし、中心角も大きいということです。
しかし、扇形の面積や、弧の長さは、円の半径の長さによって変化してしまいます。
円グラフを書く際に、半径の大きさは決まっていませんから、面積や弧の長さでは計算しにくいです。
中心角については、すべての扇形において決まっていることがあります。
中心角の合計は必ず360度です。
円グラフは、360度をどの程度に分割するかによって、数量を表すグラフともいえます。

中心角が18度だとしたら、どの程度の数量ということでしょうか。
中心角の合計は360度なので、全体を360としたときの18ということです。
「全体を〇○としたときの××」は、割合でも出てきます。
割合とは、「全体を1としたときにいくつか」ということです。
パーセントであれば、「全体を100としたときにいくつか」ということです。
「全体を360としたときの18」というのは、割合と同じことをしているんです。
まずは、割合を理解していることが、円グラフを理解することの前提になります。
「全体を360としたときの18」、これは「18は360の何個分ですか」ということです。
18÷360で割合を求めることができます。
つまり、「全体を360としたときの18」とは、0.05です。
%で表す場合は100倍をすることになるので、5%ということになります。
つまり、円グラフで中心角が18度の扇形があれば、全体の5%を意味するということです。
もう少し具体的に述べましょう。次の円グラフをご覧ください。
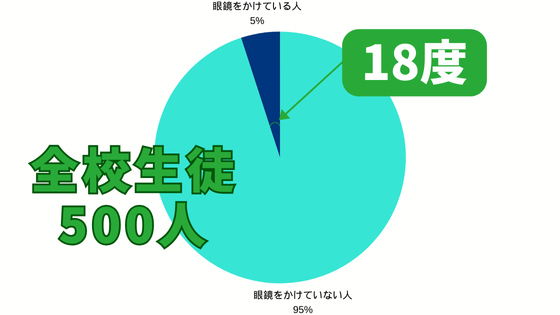
全校生徒のうち、眼鏡をかけているのが18度、つまり5%ということです。
割合が分かっていれば、眼鏡をかけている人数を求めることもできます。
全校生徒が500人なので、500×0.05=25人となります。
通常の割合であれば、割合と人数だけを使って計算することができます。
しかし、円グラフは、割合と人数に加え、中心角も使います。
割合、実際の数量、中心角、という3つの関係を理解することが求められるので、円グラフが難しいのです。
まずは、割合をきちんと理解し、そのうえで円グラフの中心角と割合の関係についても理解していきましょう。
まとめ
算数において、円グラフが出題されることがあります。
様々なグラフがありますが、円グラフが特に難しいと感じる子が多いです。
円グラフが苦手な原因として、円グラフが持つ他のグラフと異なる、中心角を使うという特徴があります。
円グラフでは、中心角の大きさによって、数量を表します。
問題を解く際には、中心角の大きさを数量に変換するなどの作業が必要になります。
円グラフの問題の解き方はいくつかありますが、割合と同じ考え方をします。
まずは割合をしっかり理解していることが必要になります。
もし割合の理解が不十分であれば、割合に戻って勉強しましょう。
割合を分かったうえで、円グラフについて問題演習など通じて理解を深めていきましょう。
算数でお困りであれば、公式LINEからお気軽にご相談ください。

また、私は家庭教師をしております。
個別指導にご興味のある方は、詳しくはこちらからご覧ください。
お読みいただき、ありがとうございます。この記事を読んで気になった方は、お気軽にご相談ください
DMやLINE公式アカウントでも個別にご相談いただけます。
Follow @twitter


![投稿についてもっと詳しく [中学受験]円すいの体積は簡単なのに、なぜ表面積は難しいのか!?](https://kawaguchiedu.com/wp-content/uploads/2019/11/14-300x169.png)




