植木算では、「本数」と「間の数」の関係を考えることが重要です。
しかし、「本数」と「間の数」の関係が抽象的なのが、苦手を生み出す原因になっています。
抽象的なので、「本数」と「間の数」の関係がイメージできないのも無理はありません。
抽象的な問題であっても、具体的に考える方法があれば解決できます。
身近なもので具体的に考える方法が、「指を広げて数える」方法です。
中学受験の大手塾に入ると、特殊算の中でも植木算を最初の頃に学習します。
最初に学ぶ特殊算である植木算で、苦手意識を持ってしまうこともあります。
一方、植木算を学習するタイミングは、算数の楽しさを知るチャンスでもあります。
植木算では、「本数」と「間の数」の関係の公式が登場します。
公式を覚えようとすると複雑ですが、覚える必要はありません。
指を広げて数えるだけで解決できます。
植木算はなぜ難しく感じるのか、指を広げて数えるとはどういうことか、述べていきます。
この記事の主な対象
- 「中学受験の算数は全く知らないけど、塾に入った最初の頃につまずかないか心配…」という方
- 「植木算って何？」という方
- 「植木算でいつも間違えてばかりで困っている」という方
- 「植木算の公式をまた忘れている…」という方
植木算とは？植木算がなぜ苦手？
植木算とは、以下のような問題のことです。
長さ800mの直線上に20mおきに木を植えます。両端にも植えるとすると木は何本必要ですか。
800÷20で、「木と木の間」が40回あります。つまり、「間の数」が40です。
そして、この「間の数」と「木の本数」の関係を考えることによって、本数を求めます。
植木算では、「間の数」と「木の本数」の関係が重要です。
「間の数」と「木の本数」という概念を理解することが必要ですが、抽象的ですよね。
植木算における「間の数」と「木の本数」には以下の関係があります。
- 両端に木を植える場合…「間の数」+1=「木の本数」
- 両端に木を植えない場合…「間の数」-1=「木の本数」
- 池の周りに植える場合…「間の数」=「木の本数」
抽象的なので、公式を覚えようとするとややこしいです。
公式を覚えるのがややこしいからこそ、植木算に苦手意識を持ってしまう子がいるのが実情です。
私自身は、小学生の頃に植木算の公式を覚えませんでした。
では、どのように解決したのでしょうか。
抽象的で分かりにくいものを、具体化することで分かりやすくできます。
公式を覚える代わりに使った方法が、「指を広げて数える」という方法です。
植木算の教え方に公式は不要！指を広げて数えるだけ！
植木算が分かりにくいのは、抽象的だからです。
具体化することができれば、分かりやすくなります。
具体化する一つの方法が「図を描く」という方法です。
5本の木がある図を描くと、間は4つあります。
間の数＋1が木の本数になっていることがわかります。
様々な図を描けば、「間の数」と「木の本数」の関係をイメージしやすくなります。
公式がなくても、図を描くことによって「間の数」と「木の本数」の関係が分かります。
図を描くことで、抽象的という植木算の難しさをカバーできるので、効果的な方法です。
しかし、毎回図を描くのは手間にもなります。
より手軽に、より身近な方法で具体的にイメージする方法が、指を広げて数える方法です。
指を広げて数える方法は、入試本番でも使うことができる方法です。
私自身も、植木算の問題を解くときは毎回指を広げて数えていました。
入試本番まで、最後まで数え続けました。
実際に数える方が覚えるよりも確実ですし、個人的には楽しんで勉強することができました。
覚えるというのは、「忘れるリスクがある」というのも重要なポイントです。
覚えること自体は悪いことではありませんが、覚えたことだけに頼るのは危険なこともあります。
それでは、実際にどのように指を広げて数えるか、3つのパターンに分けて説明していきます。
パターン① 両端に木を植える場合
指を木に見立てます。
両端に木を立てるので、親指と小指が両端になります。
「木の本数」、つまり指の本素は5本です。
「間の数」を数えると、4つです。
つまり、「間の数」は「木の本数」より1つ少ないという関係が分かります。
パターン② 両端に木を植えない場合
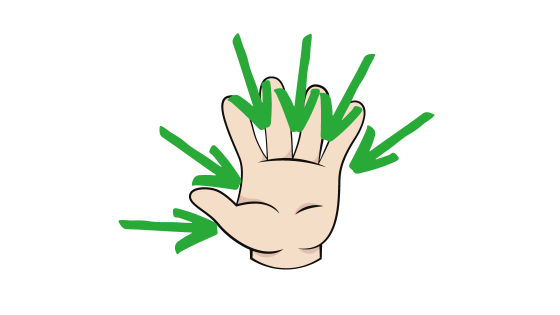
今度は、両端に木を植えないので、両端に指がないということになります
そこで、指の外側を両端だと考えます。
「間の数」は6つなので、「木の本数」より1つ多いということが分かります。
パターン③ 池の周りに植える場合
池の周りに木を植える場合でも、考え方は同じです。
指を円形に立てて、「間の数」を数えるだけです。
ちょうど野球のチェンジアップのような形にすると分かりやすいです。
チェンジアップとは、以下の様な握り方をします。
引用元：http://tkk-base.com/pitching-11
指の「間の数」を数えると、5つになります。
「間の数」と「木の本数」は同じになるということが分かります。
このように、公式がなくても、指を広げて数えるだけで解決できます。
まとめ
植木算は、中学受験の大手塾では最初の頃に学ぶ特殊算です。
ややこしさを感じる人が多いのは、抽象的だからです。
抽象的なものを、公式を覚えることで解決するのは難しいです。
図を描くことによって、具体化する方法もあります。
しかし、毎回図を描くのは手間になります。
指を広げて数える方法では、試験の現場ですぐに考えることができます。
公式を覚えなくても、「間の数」と「木の本数」の関係が分かるようになります。
公式を丸暗記しているだけでは、「解き方を忘れる」ということが待っているだけです。
忘れる心配をせずに、確実に解けるようになることを目指して勉強していきましょう。
お読みいただき、ありがとうございます。DMやLINE公式アカウントで個別にご相談いただけます。
Follow @twitter
「購読する」ボタンからPUSH通知を受け取ることができます。
お問い合わせは以下のフォームもご利用ください。
