過不足算は長椅子が難しい？[原因と対策]

過不足算は、中学受験でよく出題される特殊算の一つです。

差集め算と過不足算が似ていますから、同時期に学習することも多いでしょう。

何度も繰り返し練習するので、典型的な問題は解けるようになる人も多いです。

ところが、長椅子が登場してくる問題になると、間違える人が続出します。

私・川口も家庭教師をしていて、長椅子に悩まされる生徒を多く見てきました。

そこで、過不足算の長椅子の問題はなぜ難しいかを述べていきます。

その上で、気を付けると間違えにくくなるポイントも述べていきます。

この記事の主な対象

• 過不足算の長椅子に悩まされている方
• 過不足算の長椅子で苦労する人の悩みを知りたい方

過不足算は長椅子が難しい？

長椅子が登場しない過不足算

まずは長椅子が登場しない問題と比較してみましょう。

例えば、以下のような問題です。

リンゴを8個買うと、所持金が200円不足します。

リンゴを5個買うと所持金が100円余ります。

リンゴは1個何円でしょうか。

典型的な過不足算の問題ですね。

いくつかの解き方がありますが、線分図で解く場合を考えます。

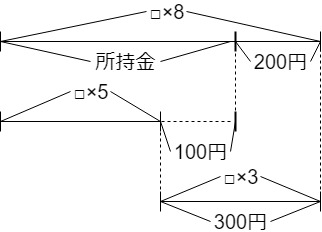
まず、リンゴ1個の値段が分からないので、□にします。

リンゴ8個を買うと所持金が不足ということは、所持金の方が200円少ないということです。

そして、リンゴ5個で所持金が余るということは、所持金の方が100円多いということです。

すると、□×8と□×5の差の部分が300円だと分かります。

□×3が300円ですから、300÷3でリンゴ1個は100円です。

1つあたりの数量が分かっていないのが、典型的な過不足算です。

長椅子が登場する過不足算

では、長椅子が登場する過不足算はどうでしょうか。

生徒が、1脚に8人ずつ座ると、3人掛けの椅子が1つできて、椅子が2つ余ります。

1脚に5人ずつ座ると、9人座れません。

椅子の数はいくつでしょうか。

問題文を読んだだけでは、大きな違いには気付かないかもしれません。

よく読むと、「1脚に8人ずつ」、「1脚に5人ずつ」というのが分かっています。

1つあたりの数量は分かっているわけです。

そして、椅子がいくつあるかが分かっていません。

リンゴの問題では、リンゴをいくつ買うかは分かっていました。

つまり、長椅子が登場する問題は、与えられる条件が逆になっています。

与えられる条件が逆になることで、図を描くときに混乱が生じます。

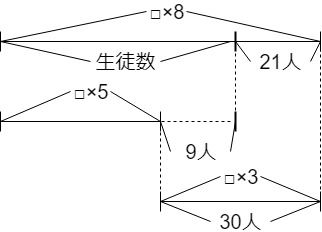
図そのものは、先ほどと似ていますね。

しかし、間違えやすいポイントがいくつかあります。

まず、長椅子の数が分からないので□にします。

□×8、これは座れる人数(座席の数)です。

椅子が余るということは、生徒数の方が少ないということです。

ところが、この「生徒数」は問題文には登場していません。

問題文に登場しないものと比べるという難しさがあります。

そして、3人掛けの椅子が1つできるということは、その椅子にはあと5人座ることができるということです。

この「5人」も問題文に登場しません。

さらに椅子が2脚ありますから、8×2で16人座れるということです。

つまり、5+16で21人分の座席が空いていることになります。

この、「21人」という問題文にない数字を考えるのも、簡単ではありません。

リンゴの問題と比較してもらえば分かりますが、「余る」を図示すると、逆になります。

リンゴの問題では、「余る」場合は、□×5が「短く」なりました。

一方、長椅子の問題では、「余る」場合は、□×5が「長く」なります。

これも混乱を招く一つの原因です。

また、「9人座れません」については、座席の数より生徒数の方が多いということです。

あとはリンゴの問題と同様に進めるだけです。

差の30人が、□×3にあたりますから、30÷3で10脚と求めることができます。

長椅子の問題で気を付けること

長椅子の問題であっても、リンゴの問題であっても、共通することはあります。

きちんと作図ができれば、間違えないということです。

問題が解けるかどうかは、作図ができるかにかかっているといえます。

では、何に気を付けて作図していけばいいのでしょうか。

まず、長椅子の問題では、基本的に生徒の人数を座席の数を比較します。

そして、「余る」は「長い」、などと丸暗記してはいけません。

生徒の人数と座席の数のどちらが多いのか、その都度考えるようにしましょう。

多い方を長くする、これが鉄則です。

生徒の人数と座席の数を比べると、さきほどの問題の「21人」のように、問題文にない数字を使う場合があります。

生徒の人数と座席の数の比較したら、どちらがいくつ多いかも考えましょう。

座席の数の方が多い場合は、「あと何人座ることができるか」と考えることが大切です。

まとめ

過不足算では、様々な問題があります。

中でも、多くの受験生を悩ませるのが長椅子の問題です。

与えられる条件が逆になるからです。

与えられる条件が逆になると、作図も逆になる部分があります。

また、問題文にない数を自分で考えて作図する必要もあります。

長椅子の問題で苦労すること自体は仕方ないことです。

しかし、長椅子の問題では、きちんと気を付ければ間違えにくくなります。

まずは、気を付けるポイントを見ながら問題を解いても構いません。

そして、練習して、見なくても自分で意識して間違えないようにしていきましょう。

その上で、意識しなくてもできるようになっていけば理想的ですね。

過不足算や算数でお困りであれば、公式LINEからお気軽にご相談ください。

また、私は家庭教師をしております。

個別指導にご興味のある方は、詳しくはこちらからご覧ください。

お読みいただき、ありがとうございます。

DMやLINE公式アカウントで個別にご相談いただけます。
Follow @twitter




「購読する」ボタンからPUSH通知を受け取ることができます。


お問い合わせは以下のフォームもご利用ください。